|
|
|
 Lebenslauf
Lebenslauf
| |
285 v. Chr. |
Über das Leben von Archimedes ist wenig bekannt.
Fest
steht, dass Archimedes den größten Teil seines Lebens in und um Syrakus
auf Sizilien verbrachte.
|
| |
212 v. Chr. |
| |

Archimedes vor seinem Tod
|
Archimedes starb während der
Eroberung von Syrakus durch die Römer im 2. Punischen Krieg. Ein
römischer Soldat drang zum alten Mann vor, als er gerade über ein
mathematisches Problem sinnierte. Der Soldat verlangte, ihn auf der
Stelle zu Marcellus zu bringen. Archimedes herrscht den Soldaten
ungeduldig an: ”Störe meine Kreise nicht!”. Das
waren seine letzten Worte, denn in blinder Wut zog der Soldat sein
Schwert und tötete Archimedes.
Sein Grabmal liess er mit einer Figur schmücken, die an seine
Erkenntnisse über das Volumen und die Oberflächen von Kugel und
Zylinder erinnern.
|
 Das Archimedische
Prinzip vom
Auftrieb
Das Archimedische
Prinzip vom
Auftrieb
|
Seine bekannteste Entdeckung, nämlich die des Auftriebs, macht er
aufgrund seiner Freundschaft mit Hieron II., dem Tyrannen von Syrakus.
Hieron wollte wissen, ob eine gekaufte Krone wirklich aus reinem Gold
war. Er bat Archimedes, den Goldgehalt der Krone zu überprüfen,
ohne sie zu beschädigen. Archimedes dachte mehrere Tage lang über das
Problem nach, aber er schien keine Lösung dafür zu finden.
Eines Nachmittags, als Archimedes gerade ein Bad
nahm, bemerkte er plötzlich, dass das Badewasser über den Rand der
Wanne schwappte. Archimedes erkannte, dass die aus der Badewanne
geflossene Wassermenge dem Volumen seines Körpers entsprach. Archimedes
lief daraufhin in Gedanken versunken und völlig nackt „Heureka“
(Ich hab's!) rufend durch die Straßen von Syrakus. Archimedes´
Erkenntnis war sehr zum Schaden des Goldschmieds: die Krone bestand zum
großen Teil aus unedlem Metall. Hieron bestrafte ihn daraufhin mit dem
Tod.
Das Archimedische Prinzip
besagt,
dass das Gewicht der verdrängten Flüssigkeit gleich gross wie das
Gewicht des schwimmenden Körper ist.
Somit wird Jeder Körper, der in eine Flüssigkeit
getaucht wird und dessen Dichte geringer als Wasser ist, nach oben
getrieben. Es entsteht Auftrieb. Schiffe gehen zum
Beispiel nicht unter, weil sie leichter sind als die Wassermenge, die
ihr Gesamtvolumen verdrängen würde.
|
 Die
Berechnung
der Kreiszahl pi Die
Berechnung
der Kreiszahl pi
Schon lange vor Archimedes war den Gelehrten
bekannt,
dass das Verhältnis zwischen Kreisumfang und Durchmesser eine Konstante
ist. Doch weder die alten Ägypter noch die Babylonier näherten sich dem
Wert der Kreiszahl Pi so genau wie Archimedes. Er berechnete Pi, indem
er versuchte, den Kreis „quadratisch“ zu machen. Dazu malte er in und
um einen Kreis Vielecke mit 6, 12, 34, 48 und 96 Seiten.
Der Umfang der Vielecke, die im Kreis lagen, wurde immer größer. Der
Umfang der Vielecke, die um den Kreis gezeichnet waren, wurde immer
kleiner. So konnte Archimedes den Wert von Pi eingrenzen. Er fand
heraus, dass Pi größer als 3,1408 und kleiner als 3,14285 sein musste.
Tabelle der ermittelten Näherungswerte
für pi:
| n-Eck |
s |
x |
a |
a*n=pi |
| 6 |
1.0000000 |
0.8660254 |
0.5176380 |
3.1058285 |
| 12 |
0.5176380 |
0.9659258 |
0.2610523 |
3.1326286 |
| 24 |
0.2610523 |
0.9914448 |
0.1308062 |
3.1393502 |
| 48 |
0.1308062 |
0.9978589 |
0.0654381 |
3.1410319 |
| 96 |
0.0654381 |
0.9994645 |
0.0327234 |
3.1414525 |
| 192 |
0.0327234 |
0.9998664 |
0.0163622 |
3.1415576 |
| 384 |
0.0163622 |
0.9999665 |
0.0081812 |
3.1415839 |
| 768 |
0.0081812 |
0.9999916 |
0.0040906 |
3.1415905 |
| 1536 |
0.0040906 |
0.9999979 |
0.0020453 |
3.1415921 |
| 3072 |
0.0020453 |
0.9999994 |
0.0010225 |
3.1415925 |
| 6144 |
0.0010226 |
0.9999998 |
0.0005113 |
3.1415926 |
|
|
|

Das rechnerische Verfahren zur
Ermittlung von pi:
| 1. |
Es
gilt
nach Pythagoras: s2=x2+(s/2)2 Für das Sechseck ist x= Für das Sechseck ist x= (3/4)=0.86602 (3/4)=0.86602 |
| 2. |
Es
gilt:
y=1-x In unserem
Fall ist y=0.13398 In unserem
Fall ist y=0.13398 |
| 3. |
Wiederum
nach Pythagoras: a2=y2+(s/2)2 Beim Sechseck also a= Beim Sechseck also a= 0.26795=0.51764 0.26795=0.51764 pi=6a=3.1058 pi=6a=3.1058 |
|
 Die Hebelgesetze
Die Hebelgesetze
Archimedes zeigte, wie ein in einem Drehpunkt
verankerter
Hebel eine schwere Last mit einer verhältnismäßig
geringen Kraft, die an einem Ende des Hebels ansetzt, heben kann.
Die Erfindung des Hebels gilt als Meilenstein in der
Geschichte der Physik. Der Hebel gehört zu den einfachen
Maschinen und überträgt eine Kraft von einem Ort auf den
anderen. Der Hebel hat viele Anwendungsmöglichkeiten.
Der Flaschenöffner ist ebenso ein Hebel wie der Nussknacker.
Beim Hebel heisst der eine Arm Kraftarm,
der andere Lastarm. Es gilt das Gesetz: Kraft x
Kraftarm =
Last x Lastarm.
Wenn der Kraftarm zum Beispiel fünfmal so lang ist wie
der
Lastarm, können wir auch eine fünfmal so schwere Last
hochheben.
Eine Anwendung des Hebelgesetzes, die Erfindung des Flaschenzuges,
wird auch Archimedes zugeschrieben.
 |
 Heureka! (Ich hab's!) Heureka! (Ich hab's!) |
 Störe meine Kreise nicht! Störe meine Kreise nicht! |
 Gib mir einen Punkt, wo ich hintreten kann, und
ich bewege die Erde! Gib mir einen Punkt, wo ich hintreten kann, und
ich bewege die Erde! |
 Es gibt Dinge, die den meisten Menschen
unglaublich erscheinen, die sich nicht mit Mathematik beschäftigt haben. Es gibt Dinge, die den meisten Menschen
unglaublich erscheinen, die sich nicht mit Mathematik beschäftigt haben. |
|
|
 Die Archimedische
Schraube
Die Archimedische
Schraube
Die archimedische Schraube, oder
auch Schraubenpumpe
genannt, diente der Bewässerung von Feldern und
Äckern. Die archimedische Schraube ist folgendermaßen aufgebaut: In
einem geteerten Zylinder aus Holzplanken dreht
sich eine hölzerne Schraube. Das untere Ende der archimedischen
Schraube liegt im Wasser. Durch die Drehbewegung
wird es nach oben befördert. Entscheidend ist dabei, dass die hölzerne
Schnecke gut an die Zylinderwand anschließt,
sonst leckt die Pumpe zu sehr. Archimedische Schrauben sind heute noch
gelegentlich im Nahen Osten und in Ägypten in
Betrieb.
 Kriegsmaschinen
Kriegsmaschinen
Archimedes letzte Jahre waren der Verteidigung
von
Syrakus gegen angreifende römische Armeen gewidmet. 3
Jahre lang belagerten die Truppen die Stadt. Immer wieder
wurden ihre Angriffe von eigenartigen Kriegsmaschinen
zurückgeworfen, die Archimedes entworfen hatte.
Eine Erfindung, die Archimedes berühmt machte, ist der Greifer
des Archimedes. Bei dieser Erfindung wird das
feindliche Boot von einem riesigen Greifarm gepackt und in Stücke
zerrissen.
Archimedes versuchte auch, Brenngläser
herzustellen, welche Schiffe mit Hilfe von gebündelten Sonnenstrahlen
vom her Land zerstören sollten. Seine Wunderwaffe sollte aus einem
sechseckigen Spiegel und kleineren viereckigen
bestehen.
 Weblinks
Weblinks
|
 back
back next
next

 Lebenslauf
Lebenslauf Das Archimedische
Prinzip vom
Auftrieb
Das Archimedische
Prinzip vom
Auftrieb
 Die Hebelgesetze
Die Hebelgesetze Die Archimedische
Schraube
Die Archimedische
Schraube Kriegsmaschinen
Kriegsmaschinen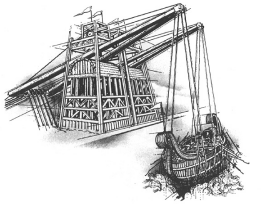

 Weblinks
Weblinks