Satz des Pythagoras
die Quadratur des Kreises
Bestimmung des Erdumfangs
Möndchen des Hyppokrates

Haupt-
seite
  

Der Satz des Pythagoras

Satz des Pythagoras Beweis

Gemäss dem griechischen Philosophen Pythagoras gilt in jedem rechtwinkligen Dreieck:

a2 + b2 = c2

 

Wobei a und b die Katheten (die am rechten Winkel anliegenden Seiten) und c die Hypothenuse (die dem rechten Winkel entgegengesetzte Seite) sind.

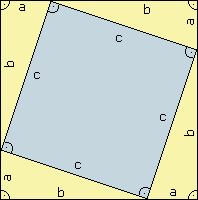
Beweis des Satzes (siehe Abbildung Links):

Die Gesamtfläche des grossen Quadrates ist (a+b)2. Diese ist gleich gross wie die Summe von c2 (Fläche des einbeschriebenen Quadrates) und 4*(ab)/2 (Summe der 4 Dreiecksflächen).

Also gilt (a+b)2 = c2 + (4*(ab)/2) a2 + 2ab + b2 = c2 + 2ab a2 + b2 = c2

Die Quadratur des Kreises

Quadratur des Kreises

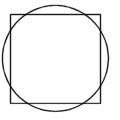
In der Antike beschäftigten sich zahlreiche Mathematiker mit der Frage, wie und ob mit Hilfe einer geometrischen Konstruktion, welche ausschliesslich Lineal und Zirkel verwendet, ein Quadrat in einen flächengleichen Kreis (und umgekehrt) verwandelt werden kann.  Die moderne Mathematik hat nachwiesen dass diese Aufgabe auch theoretisch unlösbar ist.

Erdumfang nach EratosthenesDie Bestimmung des Erdumfanges durch Eratosthenes

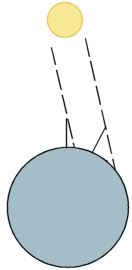
Es war der griechische Mathematiker, Philosoph und Astronom Eratosthenes (276-195 v. Chr.), welcher als erster den Erdumfang bestimmt hat. Er beobachtete die Mittagshöhe der Sonne von Alexandria und vom 787,5 km weiter südlich gelegenen Kyrene (das ist das heutige Assuan). Die Differenz der Höhen der Sonne gemessen zu demselben Zeitpunkt beträgt 7,14 Grad. Damit errechnete er den Erddurchmesser wie folgt:

787.5 km x (360 o / 7.14o) = 39'705 km

Dieser Betrag kommt dem wahren Erdumfang von ca. 40'000 km sehr nahe.

die Möndchen des Hyppokrates

Moendchen des Hippokrates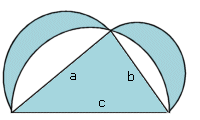Die Summe der Flächeninhalte der beiden Möndchen ist gleich gross wie die Fläche des Dreiecks:

Amo1 + Amo2 = Fabc

 

Das Dreieck ist rechtswinklig. Also gilt: a*b/2=Fabc

Die Summe der Flächen der Möndchen ist gleich Halbkreis über a + Halbkreis über b + Dreiecksfläche abc - Halbkreis über c

pi/2(a/2)2 + pi/2(b/2)2 + (ab)/2 - pi/2(c/2)2 = Fmo12

(pi/8)a2 + (pi/8)b2 + (ab)/2 - (pi/8)(c/2)2 = Fmo12

(pi/8)(a2+b2) + (ab)/2 - (pi/8)*c2 = Fmo12

da a2+b2 = c2(pi/8)c2 + (a*b)/2 - (pi/8)c2 = Fmo12(ab)/2 = Fabc= Fmo12


Sparen
Counter